警告: 整合性のない脚注開始用の簡単コード:
この警告が見当違いであれば、管理画面の 全般設定 > 脚注の開始・終了用の簡単コード > 簡単コードの整合性を検査 にある構文検査の機能を無効にしてください。
整合性のない脚注開始用の簡単コード:
“Vicky Choi. Minor-embedding in adiabatic quantum computation: I. th...www.tech.exotechblog.com2020.07.22 MASAMy favorite food is Sushi and Yakiniku.”
前回の記事では,D-Wave 2000Qにおいて,問題をキメラグラフ上にマッピングする必要があり,キメラグラフではイジングモデルのハミルトニアンに定式化された問題を解くことができる事を説明しました.
しかし,全結合型の問題を扱う場合には,グラフ問題の埋め込みが必要になります.
今回は,埋め込みの具体例を説明していきたいと思います.
グラフ問題の埋め込み
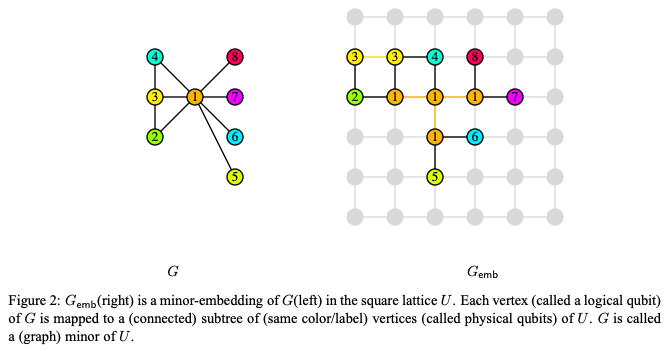
グラフ問題の埋め込みについては,Vicky Choi (2008)による論文内にわかりやすい説明がありますので,こちらの図を引用して説明します.
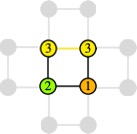
左図は,埋め込みたいグラフ構造G.
右図は簡略化したイジングモデルに,左図のグラフを埋め込んだ様子となっています.
イジングモデルにおいては,1つのノードは上下左右4つのノードとしか接続できません.
しかし,左図のノード①は7つのノードとの接続を要求しています.
このような場合は,接続のために足りないビットを複製し,複製したノード同士の相互作用は0に設定します.
例えば,ノード①,②,③同士やノード①,③,④同士は3対間相互作用を形成しています.
キメラグラフ上では2対間相互作用までしか表せませんので,擬似的に3対間相互作用を作るには,ノードを複製します.
ここでは,ノード③を複製し,ノード①と②のそれぞれに接続.
さらに,ノード③同士は,0の相互作用で接続する(相互作用を与えないとも言える)事で3対間相互作用を実現します.
同様にノード①,③,④同士の3対間相互作用を実現するために,ノード①を複製.
ノード①とノード⑤,⑥,⑦,⑧同士の2対間相互作用についても,これを実現できる分だけノード①を複製します.
イジンググラフ上でN対間相互作用の実現
3対間相互作用は,ノードを1つ増やして,4ノード使うことによって擬似的に表現できることがわかりました.
では,N対間相互作用の場合には,どうなるのでしょうか?
例えば,先ほどの図を拝借すれば,ノード①,②,③同士およびノード①,③,④同士の3対間接続に加えて,ノード②とノード④も接続すれば4対間相互作用となります.
イジングモデル上で,ノード②とノード④を接続する際にも,ダミーノードを増やせば良さそうですよね?
次回は,実際にN対間相互作用を実現するために,ダミーノードを増やしていきます.
その際,ダミーノードがどのように増えていくのか数列の漸化式を用いて表現していきましょう.

My favorite food is Sushi and Yakiniku.






コメント